Column Match Table

A column match table has an attached algorithm. The algorithm denotes the table content and how the return value is calculated. Usually this type of table is referred to as a Decision Tree.

The format of the column match table header is as follows:

ColumnMatch <ALGORITHM> ReturnType nameOfTableOrMethod(ARGUMENTS)

The following table describes the spreadsheet table header syntax:

Column match table header syntax
Element	Description
ColumnMatch	Reserved word that defines the type of the table.
ALGORITHM	Name of the algorithm. This value is optional.
ReturnType	Type of the return value.
nameOfTableOrMethod	Java valid name of the table or method as for any executable table, exposing this table in an OpenL Tablets wrapper.
ARGUMENTS	Input arguments as for any executable table.

The following predefined algorithms are available:

Predefined algorithms
Element	Reference
MATCH	MATCH Algorithm
SCORE	SCORE Algorithm
WEIGHTED	WEIGHTED Algorithm

Each algorithm has the following mandatory columns:

Algorithm mandatory columns

Column

Description

Names

Names refer to the table or method arguments and bind an argument to a particular row. The same argument can be referred in multiple rows.

Arguments are referenced by their short names. For example, if an argument in a table is a Java Bean with the some property, it is enough to specify some in the names column.

Operations

The operations column defines how to match or check arguments to values in a table. The following operations are available:

Operation	Checks for	Description
match	equality or belonging to a range	The argument value must be equal to or within a range of check values.
min	minimally required value	The argument must not be less than the check value.
max	maximally allowed value	The argument must not be greater than the check value.

The min and max operations work with numeric and date types only.

The min and max operations can be replaced with the match operation and ranges. This approach adds more flexibility because it enables the checking of all cases within one row.

Values

The values column typically has multiple sub columns containing table values.

MATCH Algorithm

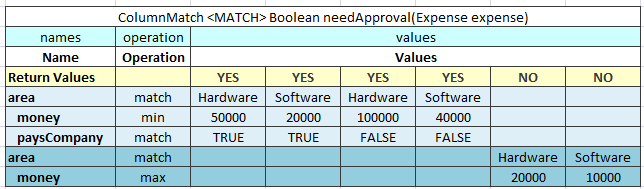
The MATCH algorithm enables the user in mapping a set of conditions to a single return value.

Besides the mandatory columns, which are names, operations, and values, the MATCH table expects that the first data row contains Return Values, one of which is returned as a result of the ColumnMatch table execution.

Figure 34: An example of the MATCH algorithm table

The MATCH algorithm works up to down and left to right. It takes an argument from the upper row and matches it against check values from left to right. If they match, the algorithm returns the corresponding return value, which is the one in the same column as the check value. If values do not match, the algorithm switches to the next row. If no match is found in the whole table, the null object is returned.

If the return type is primitive, such as int, double, or Boolean, a run-time exception is thrown.

The MATCH algorithm supports AND conditions. In this case, it checks whether all arguments from a group match the corresponding check values, and checks values in the same value sub column each time. The AND group of arguments is created by indenting two or more arguments. The name of the first argument in a group must be left unintended.

SCORE Algorithm

The SCORE algorithm calculates the sum of weighted ratings or scores for all matched cases. The SCORE algorithm has the following mandatory columns:

names
operations
weight
values

The algorithm expects that the first row contains Score, which is a list of scores or ratings added to the result sum if an argument matches the check value in the corresponding sub column.

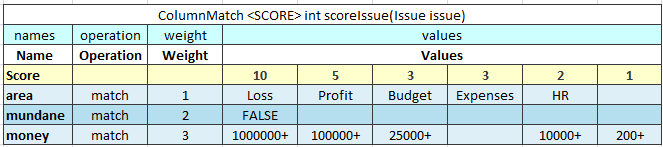
Figure 35: An example of the SCORE algorithm table

The SCORE algorithm works up to down and left to right. It takes the argument value in the first row and checks it against values from left to right until a match is found. When a match is found, the algorithm takes the score value in the corresponding sub column and multiples it by the weight of that row. The product is added to the result sum. After that, the next row is checked., The rest of the check values on the same row are ignored after the first match. The 0 value is returned if no match is found.

The following limitations apply:

Only one score can be defined for each row.
AND groups are not supported.
Any amount of rows can refer to the same argument.
The SCORE algorithm return type is always integer.

WEIGHTED Algorithm

The WEIGHTED algorithm combines the SCORE and simple MATCH algorithms. The result of the SCORE algorithm is passed to the MATCH algorithm as an input value. The MATCH algorithm result is returned as the WEIGHTED algorithm result.

The WEIGHTED algorithm requires the same columns as the SCORE algorithm. Yet it expects that first three rows are Return Values, Total Score, and Score. Return Values and Total Score represent the MATCH algorithm, and the Score row is the beginning of the SCORE part.

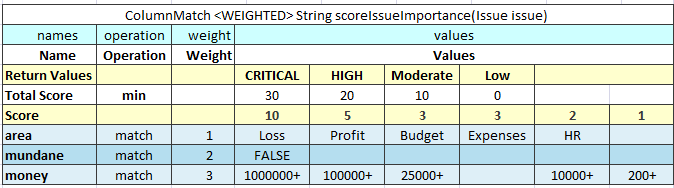
Figure 36: An example of the WEIGHTED algorithm table

The WEIGHTED algorithm requires the use of an extra Method table that joins the SCORE and MATCH algorithm. Testing the SCORE part can become difficult in this case. Splitting the WEIGHTED table into separate SCORE and MATCH algorithm tables is recommended.